Déterminer et visualiser les structures d’intérêt dans un ensemble de données grâce à l’analyse topologique
À l’occasion d’IEEE VIS 2018, conférence internationale de référence sur la visualisation de données, nous proposons une série d’articles pour découvrir différentes facettes de ce domaine. Dans ce deuxième article, nous détaillons l’analyse topologique de données, c’est-à-dire l’analyse et les propriétés des différents types d’espace des données. Cette famille d’outils mathématiques et informatiques permet d’extraire, de mesurer et de visualiser la structure de données complexes.
Avec l’essor des moyens de calcul actuels, les masses de données engendrées par les systèmes informatiques atteignent des volumes inédits, nécessitant de revoir en profondeur les méthodes d’analyse de données traditionnelles. Ce constat s’applique en particulier dans le domaine du calcul scientifique et de la simulation numérique, où les ingénieurs se doivent de simuler fidèlement un système, et ce dans un grand nombre de configurations possibles, avant de le mettre en œuvre physiquement. Par exemple, en mécanique des fluides, les ingénieurs simulent souvent un même écoulement au sein d’une pièce mécanique pour différents paramètres d’entrée (viscosité, température, vitesse). Le but est d’estimer les conditions limites d’utilisation du système en pratique mais aussi d’identifier les combinaisons de paramètres optimisant son rendement. On parle alors de “simulations d’ensemble”, où un même procédé n’est pas simulé une seule fois, mais un grand nombre de fois. Au milieu des masses de données obtenues, le but des utilisateurs est de déterminer des structures d’intérêt, c’est-à-dire des éléments particuliers à analyser. La difficulté consiste à comprendre la variabilité géométrique des structures d’intérêt au sein de leur ensemble de données, en fonction des paramètres d’entrée. Par exemple, en mécanique des fluides, le nombre, la taille et la position des tourbillons conditionnent grandement l’efficacité d’un écoulement. Dans le contexte des données d’ensemble, il devient alors capital d’identifier les différentes tendances en terme de répartition géométrique des tourbillons, et de les mettre en relation avec les paramètres d’entrée correspondantes.
De manière générale, ce problème s’apparente à la classification non-supervisée de jeux de données (comme les simulations), selon des critères relatifs aux structures d’intérêt au sein de ces données (par exemple les tourbillons).
L’analyse topologique de données offre précisément un cadre théorique et pratique pour l’extraction robuste des structures d’intérêt les plus importantes au sein d’un jeu de données. Cela permet de représenter des données complexes et volumineuses à l’aide de signatures concises et stables, sorte de cartes d’identité des structures d’intérêt. Cela facilite ainsi les tâches de comparaison et de classification. Le diagramme de persistance en est un exemple typique. Il représente les singularités présentes au sein d’un jeu de données et les associe à une mesure d’importance appelée “persistance”.
![]()
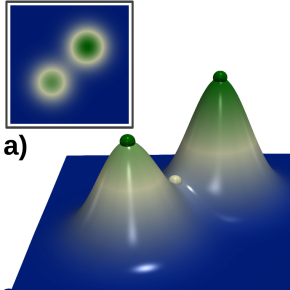
L’exemple ci-dessus représente des données synthétiques d’élévation (terrain 3D) sans bruit (a) et avec bruit (b). Le diagramme de persistance (encadré à droite) met en évidence dans les deux cas 2 singularités d’importance (barres verticales proéminentes) correspondant aux deux pics principaux présents dans les données, et ce malgré la présence de bruit en (b). Ce type de signature peut être calculé très efficacement, notamment grâce à des outils informatiques open-source tels que le “Topology ToolKit” (TTK).
Dans l’exemple de mécanique des fluides, ce type de construction permet donc d’extraire précisément la position du centre des tourbillons et de leur associer une mesure d’importance. Pour comprendre la répartition géométrique des tourbillons dans un ensemble de simulations, il ne reste alors “plus qu’à” définir des outils algorithmiques permettant de comparer des distributions de singularités associées à une mesure d’importance, comme la persistance. La publication Persistence Atlas for Critical Point Variability in Ensembles introduit des algorithmes pour la représentation et la comparaison de distributions de singularités associées à une mesure de persistance. Les chercheurs décrivent ensuite comment ces outils peuvent être utilisés à des fins de classification non-supervisée pour déterminer et visualiser les grandes tendances présentes dans l’ensemble de données.
![]()
La figure ci-dessus offre un exemple typique des visualisations rendues possibles grâce à ces outils algorithmiques. La figure de gauche (a) montre la position des tourbillons (sphère dont la taille est proportionnelle à la force du tourbillon, c’est-à-dire sa persistance) pour 5 simulations d’écoulement en 2D (1 couleur par simulation). Cette figure illustre bien la difficulté de ces données : le nombre, la position et la force de ces tourbillons varient fortement d’une simulation à l’autre. L’approche développée par les chercheurs permet précisément de comparer et de classer ces distributions de tourbillons pour identifier et visualiser les grandes tendances présentes dans l’ensemble. Elle fournit notamment une vue 2D (b) représentant la répartition des simulations dans l’espace des distributions de singularités : chaque point représente une simulation et chaque couleur une des tendances identifiées (par exemple un cluster). Cette classification permet ensuite de mener des analyses topologiques plus fines par tendance pour estimer les zones probables d’apparition des tourbillons au sein de chaque tendance. Dans cet exemple, l’approche a automatiquement identifié la présence de 5 tendances distinctes dans la répartition et le nombre des tourbillons. Les zones probables d’apparition de ces structures sont représentées par les zones colorées (illustrations de c à g).
![]()
Cette méthode est très générique et peut s’appliquer dans n’importe quel contexte applicatif où les points d’intérêt peuvent être exprimés comme les singularités d’une fonction réelle. Cette publication décrit également des exemples en sciences du climat ou en météorologie, où elle permet notamment d’identifier, au sein d’un large ensemble de simulations, différents scénarios et localisations d’évènements météorologiques, comme les trajectoires probables de dérives d’ouragans sur la côte Est américaine (image ci-dessus, 1 couleur par scénario identifié de dérive).