Des nombres à 4 dimensions pour mieux comprendre les ondes gravitationnelles
Les quaternions, des nombres généralisant les nombres complexes en dimension 4, permettent de construire une nouvelle méthode d’analyse du contenu fréquentiel et géométrique des ondes gravitationnelles et de révéler la dynamique des binaires de trous noirs coalescents. Julien Flamant s’est intéressé à ce sujet durant sa thèse réalisée au Centre de Recherche en Informatique, Signal et Automatique de Lille (CRIStAL – CNRS/Université de Lille/Ecole Centrale de Lille), pour laquelle il a reçu l’accessit du prix de thèse Signal, Image et Vision 2019.
Lorsqu’un signal porte deux informations en même temps, il est décrit par deux composantes associées à un vecteur de dimension 2 : on parle de signaux bivariés. L'évolution d’un vecteur de dimension 2 au cours du temps peut être visualisée par la trajectoire d’un trait de crayon sur une feuille de papier, voir le « gribouillis » en forme de spirale décrivant x(t) sur la figure 1. Sur cet exemple, on devine un dessin de forme circulaire : on parle de signal polarisé circulairement. La notion de polarisation est très commune en physique ondulatoire pour décrire les ondes radioélectriques ou lumineuses notamment.
L'analyse et le traitement des signaux bivariés est au cœur de nombreux domaines de la physique : analyse des ondes sismiques en géophysique, étude des propriétés des courants marins de surface en océanographie ou encore caractérisation des sources d'ondes gravitationnelles en astrophysique. Jusqu’à présent, les différents outils développés pour le traitement des signaux bivariés n’offraient pas de description simple et naturelle de ces signaux en termes de paramètres de polarisation. Afin de répondre à ces limitations, nous avons proposé une théorie unifiant interprétations physiques géométriques et outils standards du traitement du signal. En particulier, l’analyse de Fourier usuelle, qui permet de décomposer le contenu fréquentiel d’un signal (une fonction à valeurs réelles ou complexes), est construite en utilisant les nombres complexes. Elle est à la base de l'analyse spectrale, de l'analyse temps-fréquence, du filtrage linéaire, etc.
Pour généraliser cette approche aux signaux bivariés, un couple de signaux réels par exemple, nous avons proposé un nouveau cadre reposant sur les quaternions. Ces nombres hypercomplexes, introduits par Sir W.R. Hamilton au milieu du XIXe siècle, généralisent les nombres complexes en dimension 4. Ce changement de dimension fournit un nouvel espace de représentation et d’analyse. Cette représentation permet de construire un formalisme mathématique propre à l’analyse du contenu fréquentiel des signaux bivariés, tels que les ondes gravitationnelles. Bien qu’en apparence très abstraite, la nature algébrique de cette approche lui confère une interprétabilité physique remarquable. Elle permet de réaliser simplement des calculs impliquant les propriétés géométriques des signaux bivariés, sans rien sacrifier du point de vue de l’efficacité de l’implémentation numérique.
Ces résultats fournissent de nouveaux outils aux astrophysiciens pour l’étude de la dynamique orbitale des sources d’ondes gravitationnelles. Ces sources sont typiquement constituées d’une paire de trous noirs en rotation l’un autour de l’autre, tel deux danseurs : on parle alors d’un système binaire de trous noirs. Ces travaux ont été menés en collaboration avec Eric Chassande-Mottin (Astroparticule et Cosmologie APC UMR 7164 CNRS/IN2P3, collaboration Virgo). Ils reposent sur la caractérisation du motif de polarisation de l’onde gravitationnelle afin de révéler d’éventuels effets de précession orbitale du système observé. Ce sont de nouveaux détails invisibles à l’œil nu des systèmes de mesures — les interféromètres LIGO et Virgo — qui vont s’offrir à nous et aux astrophysiciens en particulier.
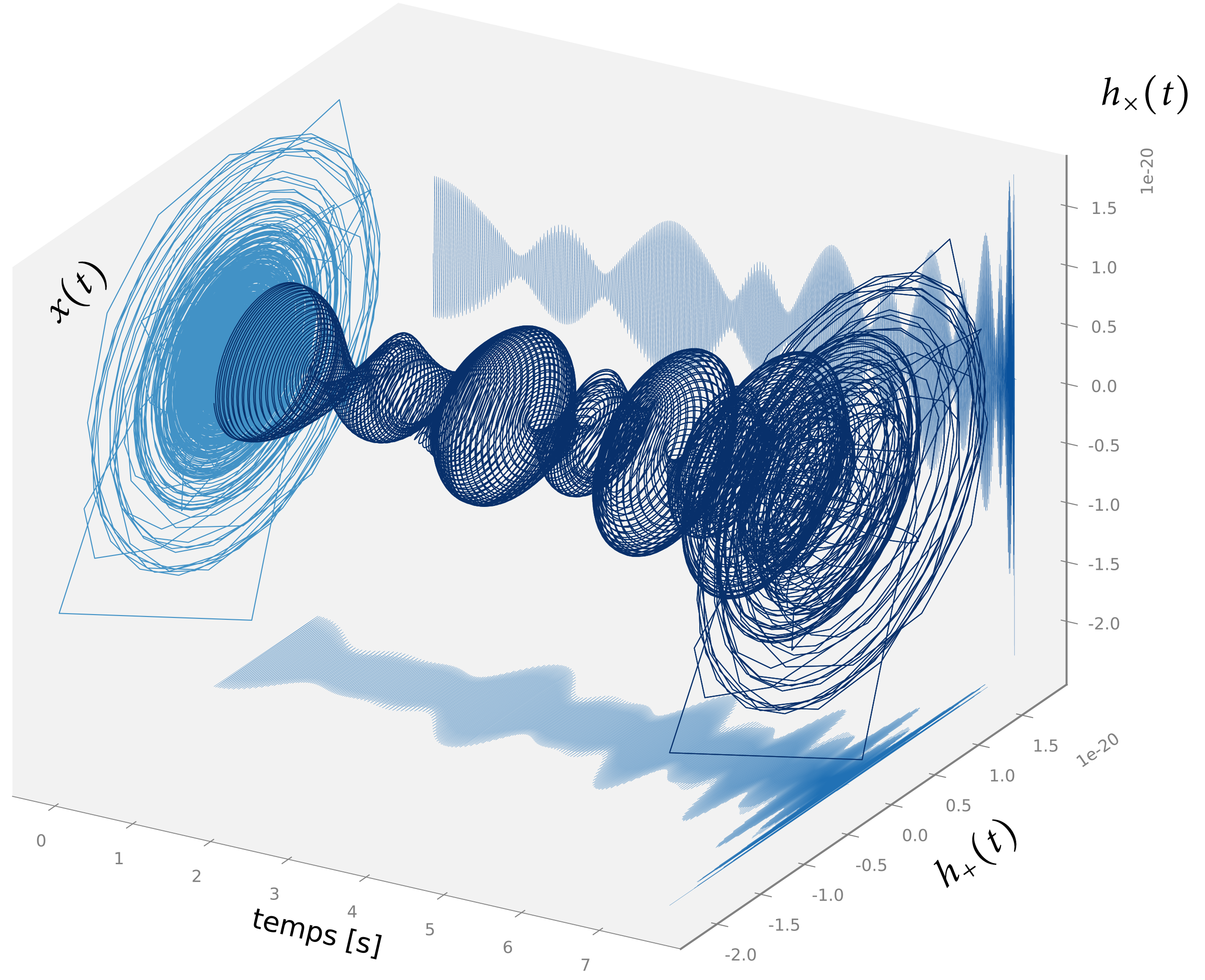
L’analyse des propriétés de polarisation instantanée de ce signal bivarié révèle la présence de précession du plan orbital de la source d’onde gravitationnelle.
Ces travaux de thèse réalisés par Julien Flamant résultent d’une collaboration entre le Centre de Recherche en Informatique, Signal et Automatique de Lille (CRIStAL – CNRS/Université de Lille/Ecole Centrale de Lille) et le laboratoire Grenoble Images Parole Signal Automatique (GIPSA-Lab – CNRS/Grenoble INP/Université Grenoble Alpes). Ils ont été partiellement financés par le CNRS et le GdR ISIS au travers du projet SUNSTAR.
Julien Flamant est désormais chercheur en post-doctorat au sein du Centre de Recherche en Automatique de Nancy (CRAN - CNRS/Université de Lorraine).
Référence
"Une approche générique pour l’analyse et le filtrage des signaux bivariés"