Résumer de grandes masses de données grâce aux signatures topologiques moyennes
À l’occasion de IEEE VIS 2019, conférence internationale de référence sur la visualisation de données, des chercheuses et chercheurs proposent une série d’articles pour découvrir différentes facettes de ce domaine. Julien Tierny, chargé de recherche CNRS au Laboratoire d'informatique de Paris 6 (LIP6 - CNRS/Sorbonne Université), détaille une nouvelle méthode pour l’analyse des propriétés structurelles des données. Ce type d’outils mathématiques et informatiques permet d’extraire, de mesurer et de visualiser la structure de données complexes.
À l’ère des big data, les données générées par notre activité numérique sont de plus en plus complexes, volumineuses et nombreuses. Leur analyse et leur compréhension deviennent donc de plus en plus difficiles et il est nécessaire de concevoir des outils informatiques avancés pour résoudre ce problème. Pour comprendre un jeu de données, un analyste est souvent confronté aux questions suivantes : comment extraire l’information utile au sein d’un jeu de données ? Comment comparer et organiser des jeux de données sur la base de leur information utile ?
Par exemple, une opération fréquente en analyse de données est le partitionnement (“clustering” en anglais), qui consiste à regrouper des jeux de données similaires au sein d’un même groupe. Malheureusement, lorsque la taille des données augmente, ce problème devient notoirement difficile : la malédiction de la dimension, phénomène bien connu en analyse de données, opère pleinement et les méthodes traditionnelles peinent à identifier des groupes pertinents. Pour faire face à ce problème, il est nécessaire de considérer des points de vue radicalement nouveaux.
L’Analyse Topologique de Données est un domaine de recherche récent en informatique, qui se focalise sur la découverte des structures cachées au sein des données (comme par exemple des motifs périodiques). Un aspect pour lequel ce type d’outil excelle est le calcul de descripteurs structurels concis de larges volumes de données.
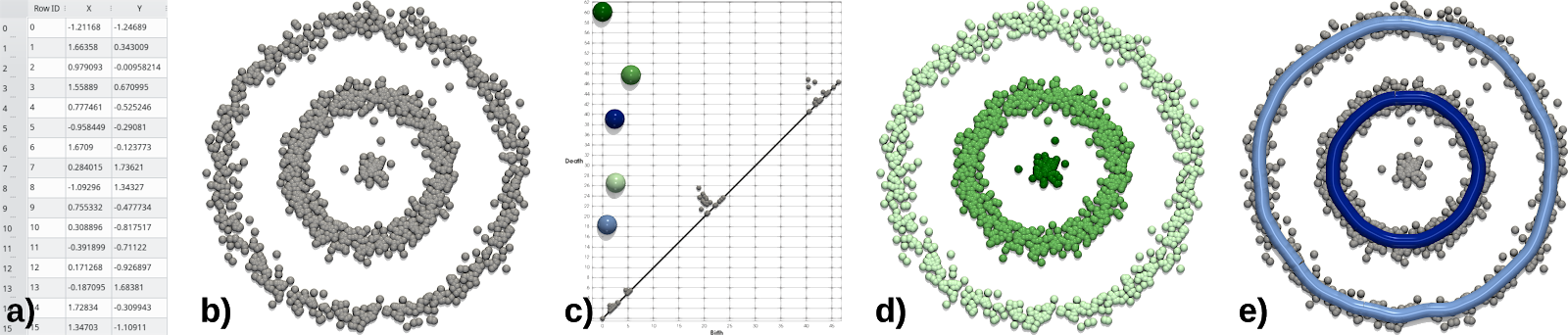
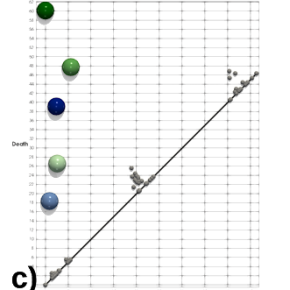
De manière générale, comme illustré ci-dessus, un jeu de données (a) peut être représenté par un nuage de points (b). Le diagramme de persistance (c) est un outil typique en analyse topologique de données, qui peut être interprété comme une “signature topologique” du jeu de données. En particulier, il fournit des informations utiles décrivant la structure du nuage de points (b). Chaque point dans ce diagramme (c) représente une structure topologique et sa distance par rapport à la diagonale (en noir) dénote son importance dans les données. Dans la figure ci-dessus (c), les points verts représentent les parties indépendantes (d) des données (leurs “composantes connexes”), tandis que les points bleus représentent les structures périodiques (e) principales (cycles indépendants). Le diagramme de persistance résume donc le jeu de données ci-dessus en cinq structures topologiques principales (c), décrivant les trois parties indépendantes en vert (d), qui s’avèrent former deux cycles en bleu dans cet exemple (e). Cet outil permet donc de visualiser et d’analyser facilement les propriétés structurelles d’un jeu de données. Par ailleurs, il peut se calculer efficacement grâce à des logiciels open-source comme le “Topology ToolKit”.
En pratique, un analyste est rarement confronté à un unique jeu de données. Il doit, dans la plupart des cas, considérer de larges collections de jeux de données (par exemple, pour décrire des phénomènes structurels au sein de populations). Il se pose alors la question de savoir, étant donné un ensemble de jeux de données, quelle est la signature topologique qui représente au mieux cet ensemble ? Autrement dit, quelle est la signature topologique moyenne de la base de données ?
Il s’agit là d’une question fondamentale ayant des applications directes en visualisation (pour l’interprétation visuelle de grandes collections de jeux de données) et en analyse de données (comme pour le problème de partitionnement évoqué ci-dessus).
Cette question est précisément l’objet de la publication “Progressive Wasserstein Barycenters of Persistence Diagrams”, rédigée par des chercheurs du LIP6 et primée à la conférence IEEE VIS 2019. Ce travail montre comment étendre des résultats récents venant du transport optimal (autre outil mathématique très étudié actuellement) aux signatures topologiques, et ainsi comment générer des signatures topologiques moyennes, et ce, en temps interactifs !
Par ailleurs, le calcul de moyennes est une opération de base utilisée par les algorithmes de partitionnement, comme le k-means. Cette publication décrit également comment étendre ces algorithmes de partitionnement pour qu’ils puissent opérer sur des collections de signatures topologiques.
En termes d’applications, cet outil promet une ouverture du champ des possibles dans les domaines des sciences du climat et en météorologie, comme dans la figure ci-dessous, qui illustre le partitionnement d’une collection de simulations d’ouragans sur la côte Est américaine. Dans cet exemple, le partitionnement discerne automatiquement les simulations relevant (de gauche à droite) de la formation, de la dérive et de l'atterrissage de l’ouragan. La signature topologique moyenne de chacun de ces groupes (en bas) permet d’identifier visuellement le nombre et la force des zones de vents violents (en vert).
Tous les algorithmes présentés dans cette publication sont désormais disponibles dans la bibliothèque open-source “Topology ToolKit”.
