L’heureux mariage du calcul formel et de l’optimisation

L’amélioration des algorithmes utilisés dans la reconstruction de volumes constitue un progrès pour les nombreuses technologies qui y ont recours, comme l’imagerie médicale. Mioara Joldes et Jean-Bernard Lasserre du Laboratoire d’Analyse et d’Architecture des Systèmes du CNRS (LAAS-CNRS), ainsi que Florent Bréhard, ancien doctorant du LAAS-CNRS et de l’ENS Lyon, et actuellement post-doctorant en Suède à l’université d’Uppsala, ont obtenu le prix du Distinguished Paper Award pour leur nouvelle approche dans le domaine, fondée sur la théorie des fonctions holonomiques. Il leur a été remis au mois de juillet lors de l’International Symposium on Symbolic and Algebraic Computation (ISSAC) à Pékin.

 Méconnues du grand public mais très prisées en calcul formel, les fonctions holonomiques sont les solutions des équations différentielles1 dont les coefficients sont des polynômes. Cette propriété particulière permet de les représenter et de les manipuler de manière exacte, grâce à des algorithmes efficaces.

« Environ 60 % des fonctions de l’ouvrage de référence Handbook of Mathematical Functions2 sont holonomiques, affirme Mioara Joldes. Les chercheurs en calcul formel développent des algorithmes pour les calculer de manière uniforme et en obtenant une réponse exacte. Cela évite les risques d’erreurs en parcourant un livre et en recopiant des tables de valeurs. »

• 1Les équations différentielles sont des équations mettant en relation une fonction inconnue à déterminer avec ses taux d’accroissement, que l’on appelle dérivées.
• 2Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, à l’origine sous la direction de Milton Abramowitz et Irene Stegun.

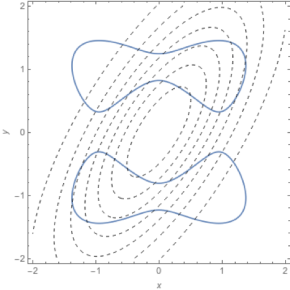
Si Jean-Bernard Lasserre est réputé pour ses travaux en optimisation, Mioara Joldes et son ancien doctorant Florent Bréhard traitent du calcul formel. Leur publication primée, On moment problems with holonomic functions, présente un nouvel algorithme permettant la reconstruction de formes à partir de données non spatiales, appelées moments. À titre d’exemple, des appareils comme un tomographe ou une IRM ne relèvent en effet pas des positions sur l’objet étudié, mais des informations sur la façon dont celui-ci réagit lorsqu’il est soumis à une onde émise par la machine. En multipliant les mesures à des fréquences différentes, on obtient suffisamment de moments pour procéder à la reconstruction.

Dans l’algorithme proposé, la théorie des fonctions holonomiques permet de remonter à la forme produisant de tels moments, qui est celle de l’objet étudié. La nouveauté de ces travaux tient dans le fait qu’ils fonctionnent également si la cible n’est pas uniformément dense et que, au-delà de leur seule forme, ses parties ne répondent pas toutes de la même manière à la sollicitation. Ces variations de densité sont alors elles aussi mesurées et fidèlement reproduites.

« Ce prix donne une visibilité à l’étude des problèmes de moments avec des outils issus du calcul formel, se félicite Mioara Joldes. Nous avons montré que des objets algébriques pouvaient avoir un intérêt pour une reconstruction numérique efficace. » Présentés à la conférence ISSAC, ces algorithmes ouvrent la voie à des travaux complémentaires.

Les instruments physiques produisent par exemple des mesures forcément sujettes à une marge d’erreur, qui impacte les moments et donc la fidélité de la forme reconstruite. Les chercheurs vont donc continuer à utiliser des outils du calcul formel et de l’analyse numérique pour étudier ces aspects et proposer d’autres applications potentielles.

Références :

Florent Bréhard, Mioara Joldes, Jean-Bernard Lasserre. On Moment Problems with Holonomic Functions. ISSAC 2019 - 44th International Symposium on Symbolic and Algebraic Computation, Jul 2019, Pékin, China. pp.66-73. ⟨hal-02006645⟩