Un ERC face au challenge du big data
À cause d’un phénomène appelé « malédiction de la dimension », de nombreux outils mathématiques et informatiques ne fonctionnent plus face aux grandes masses de données. Fort d’une bourse ERC Consolidator, Julien Tierny du LIP6 conçoit des algorithmes adaptés à un tel flot d’informations. Ses travaux, toujours sous le sceau de l’open source, seront optimisés pour les supercalculateurs et offriront des outils topologiques pour l’analyse de vastes bases de données.
Difficile d’échapper au big data, un terme sur toutes les lèvres pour désigner l’explosion de la quantité de données disponibles. Comme la hausse continue de la puissance des ordinateurs ne suffit pas à maîtriser le phénomène, des scientifiques comme Julien Tierny conçoivent des programmes spécifiquement pour gérer ce flot. Chargé de recherche CNRS au LIP6 (LIP6, CNRS/Sorbonne Université), ses travaux viennent d’atteindre un nouveau palier avec l’attribution d’une bourse ERC Consolidator pour son projet TORI1 .
Celui-ci s’inscrit dans la droite lignée des travaux reconnus de Julien Tierny sur la topologie des données, ou comment retrouver de la structure au sein de grands jeux de données, pour faciliter leur visualisation, leur analyse et leur interprétation. Cet objectif trouve des applications dans tous les domaines où l’on manipule de grandes quantités de données, mais Julien Tierny se focalise sur les bases de données scientifiques obtenues par des simulations numériques ou des collectes d’information. Il aide par exemple des chimistes à mieux comprendre les interactions entre molécules. À une tout autre échelle, cela sert également en astrophysique, où les chercheurs scrutent les connexions entre clusters de galaxies au sein de la toile cosmique. Enfin, ces travaux peuvent s’appliquer à la mécanique des fluides, aux sciences du climat, à la physique des solides, la géologie… Des entreprises comme EDF ou Total font aussi appel à ses talents.
Au-delà d’une simple question de puissance de calcul qui ferait défaut, l’enjeu est d’autant plus important que rôde l’ombre de la malédiction de la dimension. Identifié par le mathématicien américain Richard E. Bellman (1920 – 1984), cet ensemble de problèmes apparaît lorsque l’on manipule des données dans des domaines de trop grandes dimensions. En particulier, la masse d’information finit par faire perdre tout sens aux outils mathématiques classiques.
« Quand on compare deux images, le plus simple consiste à mesurer la différence entre tous les pixels, explique Julien Tierny. Cela revient à mesurer la distance euclidienne entre deux points dans un espace qui aurait autant de dimensions qu’il y a de pixels dans chaque image. À force d’augmenter la taille des images, la dimension augmente et la distance euclidienne traditionnelle dans de tels espaces n’est plus suffisamment discriminante pour être informative. »
L’analyse topologique de données ouvre de nouvelles perspectives en cherchant d’autres types de distances, opérant sur des signatures topologiques des données, qui capturent particulièrement bien leur structure principale. Ces objets topologiques, comme le diagramme de persistance (Figure 1) ou le graphe de Reeb (Figure 2) ou le complexe de Morse-Smale, sont des représentations plus concises que les données brutes, et donc plus pratiques à manipuler pour des algorithmes. Elles décrivent cependant bien l’information structurelle intrinsèque des données, dont elles forment la substantifique moelle.
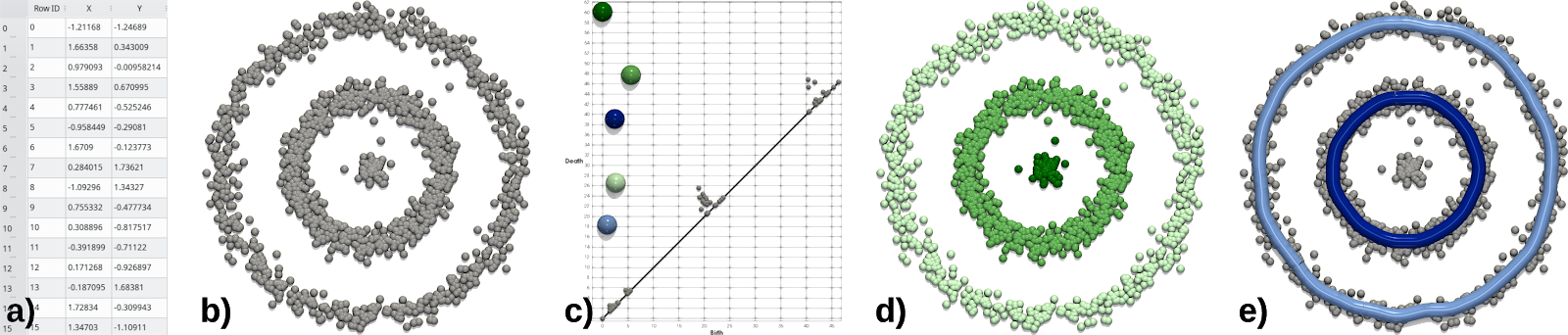
Dans le projet TORI, l’enjeu n’est plus d’utiliser ces outils topologiques pour l’analyse d’un seul jeu de données, mais pour l’analyse statistique d’ensembles de jeux de données. Cela dans le but de comprendre les structures récurrentes au sein de grandes bases de données scientifiques typiquement générées aujourd’hui, ou au contraire, d’identifier des anomalies.
Les algorithmes développés depuis une vingtaine d’années ont donc besoin d’être réécrits pour faire face à cette nouvelle réalité. Mieux, TORI vise à offrir des méthodes informatiques pour produire des statistiques sur la structure d’ensembles de bases de données, parfois complètement indépendantes. Ces différents outils seront également adaptés au contexte haute performance, c’est-à-dire qu’ils seront optimisés pour fonctionner sur des supercalculateurs.
« J’ai d’abord cru à une erreur lorsque la bourse ERC m’a été confirmée, s’amuse Julien Tierny. Passé l’effet de surprise, je me suis rendu compte que c’est une opportunité unique de monter une petite équipe pour faire progresser significativement ces sujets. J’ai l’impression de monter une start-up ! » Le financement européen assure un changement d’échelle du projet, mais le chercheur ne perd pas de vue sa vision première de l’informatique.
L’ensemble des travaux issus de TORI sera implémenté dans des logiciels open source, dans une démarche de science ouverte à 100 %. Un Topology ToolKit est déjà disponible et sera continuellement amélioré, le « réceptacle et la vitrine » du projet selon Julien Tierny. « Les retombées du projet doivent être utilisables par tout le monde, rapidement et facilement. »

→ En savoir plus sur les travaux de recherche de Julien Tierny
Contact
Notes
- In-situ Topological Reduction of Scientific 3D Data, réduction topologique in situ de données scientifiques 3D.
