Maks Ovsjanikov, ERC Starting Grant 2017
Les formes 3D se multiplient, mais leur manipulation n’est pas nécessairement devenue plus aisée. En effet, comment comparer une silhouette d’homme en nuage de points, avec un autre représenté par un maillage de triangles ? Comment détecter leurs similitudes et différences, le tout avec une vitesse d’exécution acceptable pour l’utilisateur ? Maks Ovsjanikov, maître de conférences à l’École polytechnique et membre du Laboratoire d’Informatique de l’École polytechnique (LIX - CNRS/École polytechnique), travaille sur cette problématique dans le cadre de son ERC Starting Grant EXPROTEA.
Les images ou objets 3D deviennent de plus en plus courants. Quelles problématiques restent encore à résoudre ?
Maks Ovsjanikov : Il est vrai qu’il y a maintenant à disposition de tout un chacun de grandes bases de données de modèles 3D, comme 3D Warehouse ou Shapenet par exemple. Les domaines qui produisent des objets 3D sont également de plus en plus nombreux. Il y a évidemment les effets spéciaux de films ou de jeux, ou la conception assistée par ordinateur pour la fabrication industrielle, mais aussi le développement d’objets 3D produits dans les FabLab avec des procédés de fabrication additive, des données issues de l’imagerie médicale ou encore de la préservation du patrimoine culturel, notamment en archéologie. Les bases de données typiques contiennent aujourd’hui des milliers voire des millions de formes 3D.
L’un des principaux objectifs de ma recherche est de développer des algorithmes qui permettront de quantifier la similitude entre des formes. Par exemple, à partir d’un objet 3D, pouvons-nous créer un algorithme qui pourrait trouver des formes similaires dans une grande base de données ? Est-il possible de trouver des points ou même des parties similaires ou différentes entre deux images 3D ? En d’autres termes, pouvons-nous concevoir des algorithmes permettant de révéler les relations et la variabilité qui existent dans les collections de formes 3D ?
Pour répondre à ces questions, nous devons nous attaquer à deux problèmes clés. Tout d’abord, les algorithmes que nous développons doivent être suffisamment efficaces, rapides, pour pouvoir gérer de vastes quantités de données. En effet, un seul objet 3D peut contenir des milliers, des millions de points ! Le comparer à des millions d’autres est une tâche difficile, pour autant l’utilisateur n’acceptera pas d’attendre très longtemps.
Seconde problématique, les données géométriques des objets 3D peuvent être exprimées dans des représentations différentes, qu’il s’agisse de nuage de points, de maillages en triangles ou encore de quadrillages. Les méthodes que nous créons doivent donc pouvoir accueillir ces différents types de données.
Pour résoudre ces deux problèmes, notre intuition est « d’oublier » la nature des données, et de les abstraire pour exploiter ce qu’on appelle leurs espaces fonctionnels.

© M. Ovasjanikov
Comment se construisent les espaces fonctionnels des objets 3D ? Et comment les manipule-t-on ?
M. O. : Si l’on prend l’exemple d’un nuage de points, on peut les traiter comme des points isolés, comme ce que l’on faisait jusque-là, ou alors associer une valeur réelle à chaque point et ainsi définir la fonction qui correspond à ces points. Cette fonction peut exprimer une propriété physique (par exemple, la température à chaque point) ou une quantité géométrique telle que la courbure. En oubliant la nature des points (ce qui résout ainsi le problème des représentations différentes en points ou en maillages), on se concentre sur les fonctions qui peuvent se dessiner sur différents espaces. Les points étaient jusque-là limités dans une représentation, qui empêchait les comparaisons avec d’autres formes d’expressions de points (triangles, quadrillage), alors que les espaces des fonctions gardent tous les potentiels géométriques des points, mais ouvrent à toutes les comparaisons. Cela crée une représentation, un cadre uni pour exprimer les propriétés géométriques des objets.
Au-delà de dépasser les différences d’expression entre nuages de points et maillages, cette abstraction permet également des calculs beaucoup plus efficaces car les ordinateurs savent traiter facilement les nombres réels et les sommes et multiplications sur des fonctions. Les fonctions à valeur réelle ont une structure algébrique riche, qui peut être ainsi utilisée pour développer des algorithmes plus efficaces. Les fonctions sont réduites à des fonctions de base afin que leur combinaison soit la plus simple possible à traiter.
Enfin, cette abstraction permet également de considérer un objet 3D comme un « opérateur ». Nous avons établi qu’une fonction était comme une liste de valeurs, une pour chaque point. Si l’on doit modifier l’ensemble de ces valeurs, si une liste devient une autre liste, ce changement est réalisé par ce que l’on appelle un opérateur. Ce que je propose d’exploiter dans mon projet c’est le fait que beaucoup de propriétés géométriques, des objets en général en 2 ou 3D, peuvent être encodées comme des opérateurs. Dans un sens, les opérateurs nous donnent un autre langage pour exprimer les propriétés différentes des objets sans être sensible à leurs représentations de départ.
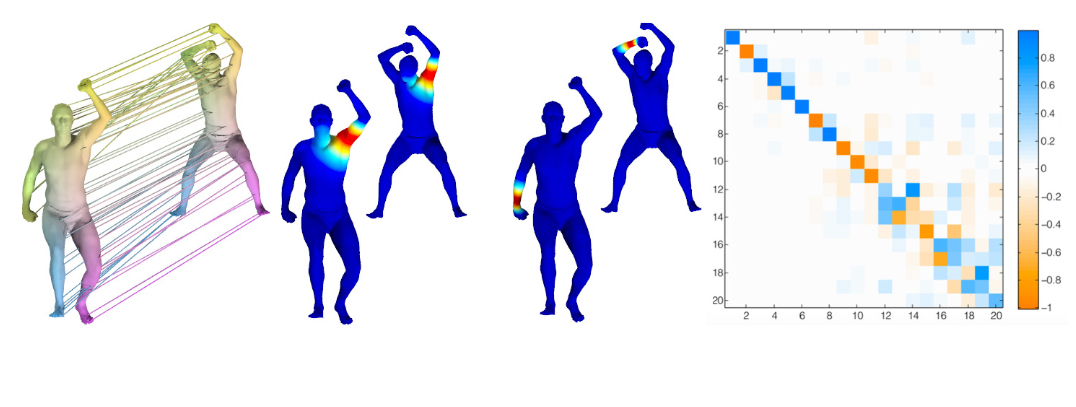
© M. Ovsjanikov
Où en êtes-vous actuellement dans votre projet ?
M. O. : Le but général est de définir des objets plus abstraits que les objets 3D de départ, car cette représentation permet de réunir plusieurs propriétés et plusieurs domaines d’application. Cette abstraction permet de mieux saisir l’essence de l’objet. Nous pouvons ainsi créer un nouveau cadre pour analyser et traiter des données géométriques efficacement dans de nombreuses représentations différentes et en exprimant différentes opérations dans la même langue.
Nous avons déjà obtenu des résultats préliminaires prometteurs dans cette direction. Je travaille d’ores et déjà avec des données d’anatomie comparée issues du Muséum d’histoire naturelle. Au niveau de la paléontologie, un projet consiste à comparer des os d’animaux différents, et de détecter des régions où il y a des différences ou des similarités.
