Un nouveau filtre à sauts flous pour le débruitage de séries temporelles
Comment analyser des séries temporelles de données qui sont imparfaites et incertaines ? Le travail de chercheurs du LIRIS, de SAMOVAR et de Dhofar Université à Oman les a conduit à étudier des séries chronologiques présentant des transitions progressives entre deux états, comme des températures mesurées durant des alternances jour/nuit. Pour répondre à ce type de problème, les chercheurs ont mis au point un nouvel algorithme exact et rapide de la famille des filtres de Kalman qui prend en compte des états flous. Ces travaux sont présentés dans IEEE Transactions on Fuzzy Systems du 10 juin 2019.
Commençons par le commencement : qu’est-ce qu’un filtre de Kalman ? Le filtre de Kalman est un algorithme d’estimation optimal. Il est principalement utilisé dans deux configurations :
- Pour estimer l’état d’un système lorsqu’il ne peut pas être mesuré directement. Exemple : comment contrôler la température à l’intérieur de la chambre de combustion d’un moteur lorsque les températures sont extrêmes ; par des mesures indirectes à l’extérieur de la chambre.
- Pour estimer l’état d’un système en combinant des observations provenant de différentes sources de données imparfaites. Exemple : le capteur inertiel d’un smartphone et l’odomètre d’un véhicule fournissent des positions relatives et les données GPS une position absolue. À quelle position se situe un véhicule à l’intérieur d’un tunnel, c’est-à-dire lorsque les données GPS deviennent elles-mêmes approximatives ?
Les applications les plus communes du filtre de Kalman concernent les systèmes de navigation, le traitement d’images (poursuite d’objet dans les vidéos) et le traitement du signal. L’une des toutes premières applications de ce filtre est associée à la mission Apollo et au guidage de la navette vers la lune dans les années 1960.
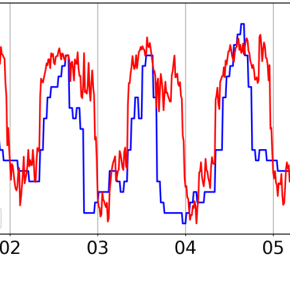
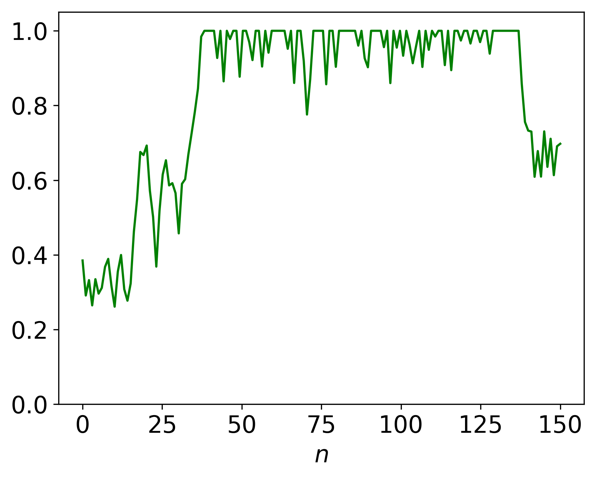
Ce travail se situe dans le cadre d’une série de travaux commencés dans les années 2000 qui étudie certaines extensions de ce filtre, tout en conservant l’optimalité et la rapidité de l’algorithme obtenu. Lorsque les observations dépendent de plusieurs modes, comme lors de la poursuite de cibles durant une alternance jour/nuit, le filtre est dit à sauts. Dans ce contexte, l’originalité du travail consiste à intégrer des sauts flous, par le biais de lois de probabilité mixtes discrète / continue, en combinant mesure de Dirac et mesure de Lebesgue. À titre d’illustration, la trajectoire simulée d’une chaîne de Markov à sauts flous est représentée dans la figure 1.
Dans la pratique, il existe de nombreuses situations où une représentation par sauts durs ‘0’ et ‘1’ n’est pas suffisante. Prenons l’exemple suivant, où l’on cherche à expliquer la consommation d’énergie d’un bâtiment à partir de mesures sur la température extérieure (figure 2). Nous sommes typiquement dans la première configuration d’usage des filtres de Kalman.
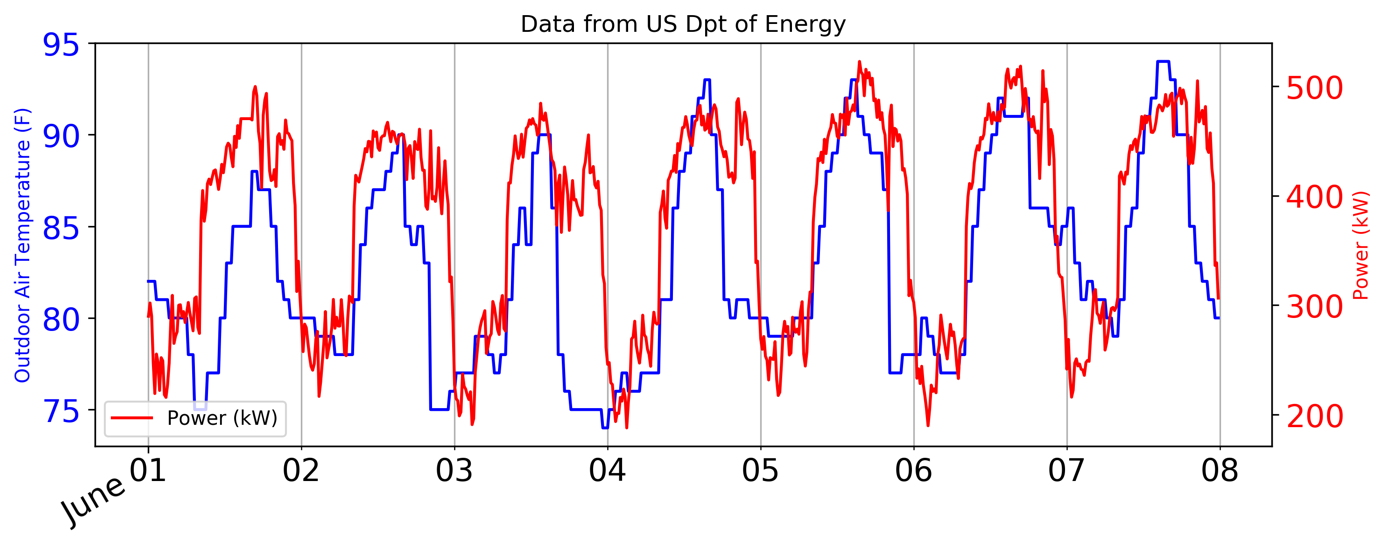
Le profil journalier typique de la température extérieure présente une forme avec deux paliers : ces paliers sont atteints lors des températures les plus basses et les plus hautes de la journée, typiquement entre 1h et 5h, et entre 13h et 17h. Entre ces paliers les températures augmentent ou diminuent progressivement. Pour traiter ces données avec le filtre proposé, les chercheurs ont considéré que les observations modélisent la température extérieure alors que les états modélisent la consommation d’énergie.
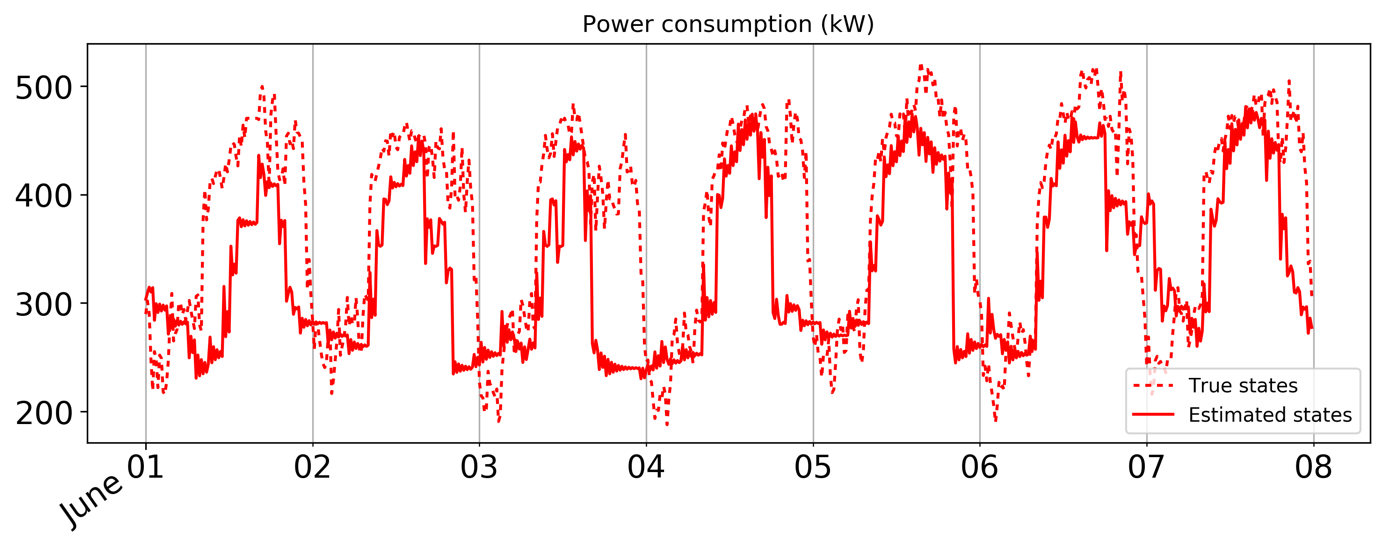
En termes de résultat, le calcul de l’erreur quadratique moyenne, l’un des critères pour lequel le filtre de Kalman est optimal, montre une amélioration notable des résultats par rapport à une modélisation plus classique à sauts durs. La figure 3 illustre la qualité de l’estimation de la consommation d’énergie obtenue par le filtre, par comparaison avec la vérité-terrain.
Papier
Z. Bouyahia, S. Derrode and W. Pieczynski, Filtering in Gaussian Linear Systems with Fuzzy Switches, IEEE Trans. on Fuzzy Systems, accepted June 2019.