Un dé pipé aux multiples facettes pour améliorer les moteurs de recherche

Imaginez que vous êtes un moteur de recherche d’images, et qu’un utilisateur vous soumet une requête intitulée « midi ». Vous devez lui proposer des objets pertinents pour sa recherche. En même temps, sa recherche est ambigüe : souhaite-t-il avoir des informations sur le découpage du temps, ou sur une zone du sud de la France ? Pour augmenter vos chances de répondre utilement à l’utilisateur, vous devez donc non seulement être pertinent pour sa requête, mais aussi proposer des réponses diverses qui couvrent tous les sens possibles du mot « midi ». 

Pour répondre à ce besoin, les chercheurs de Zonotope hit-and-run for efficient sampling from projection DPPs utilisent un outil probabiliste appelé processus déterminantaux (DPP, pour determinantal point process). Pour bien comprendre ce qu’est un déterminant, élément à la base des DPP, il faut imaginer que les chercheurs représentent chaque réponse à une requête (ici, chaque image d’un grand ensemble d’images) par un vecteur. La longueur de chaque vecteur correspond à la pertinence de la réponse pour la requête. Dans l’exemple ci-dessous, les images sont toutes pertinentes pour la requête « midi », et donc correspondent à de grands vecteurs. Les chercheurs vont ensuite mesurer la dissimilarité entre deux réponses, donc entre deux vecteurs, comme la surface bleue dans l’exemple ci-dessous. L’aire de cette surface bleue est appelée déterminant des deux vecteurs. Plus les réponses sont diverses, plus la surface bleue est étendue, plus le déterminant est important. De la même manière, plus une réponse est individuellement pertinente, plus la longueur du vecteur correspondant est grande, et donc plus les surface bleues qui utilisent ce vecteur sont grandes. On comprend donc que les grandes zones bleues correspondent à des couples d’images qui sont à la fois individuellement pertinentes et diverses.

De plus, de la même façon qu’un point peut être défini par une abscisse et une ordonnée dans un plan à deux dimensions, une réponse à une requête peut être définie par un vecteur dans un espace de dimension plus grande que deux : chaque vecteur est maintenant décrit par un nombre de coordonnées arbitraire appelé d. On peut alors généraliser l’idée de zone bleue à une boîte en dimension d, dont le déterminant mesure le volume. Ce déterminant donne encore une mesure de la pertinence individuelle et de la diversité des d vecteurs qui forment les arêtes de cette boîte. Le but du moteur de recherche étant de fournir des réponses pertinentes, mais aussi diverses, il faut donc que les différentes réponses fournies forment une zone bleue avec le plus grand déterminant possible. 

Problème : il est mathématiquement impossible de déterminer en un temps raisonnable le sous-ensemble de d images correspondant au plus grand déterminant. Par contre, il est possible de faire presque aussi bien, grâce aux DPP. Dans notre exemple, le DPP est la représentation de toutes les surfaces bleues combinées dans cet espace de dimension très grande, comme un dé dont chaque face est une des nombreuses surfaces bleues. Chaque lancer de ce dé fait ressortir un nouveau sous-ensemble de réponses, et le DPP est un dé pipé : on obtient plus souvent les ensembles avec de grands déterminants. En pratique, il est possible de programmer un tirage de DPP sur un ordinateur de bureau lorsque l’ensemble de toutes les images n’excède pas quelques milliers. Pour les applications à de plus grands volumes de données (pensez au nombre d’images sur internet…), tirer un DPP reste impossible en pratique. 

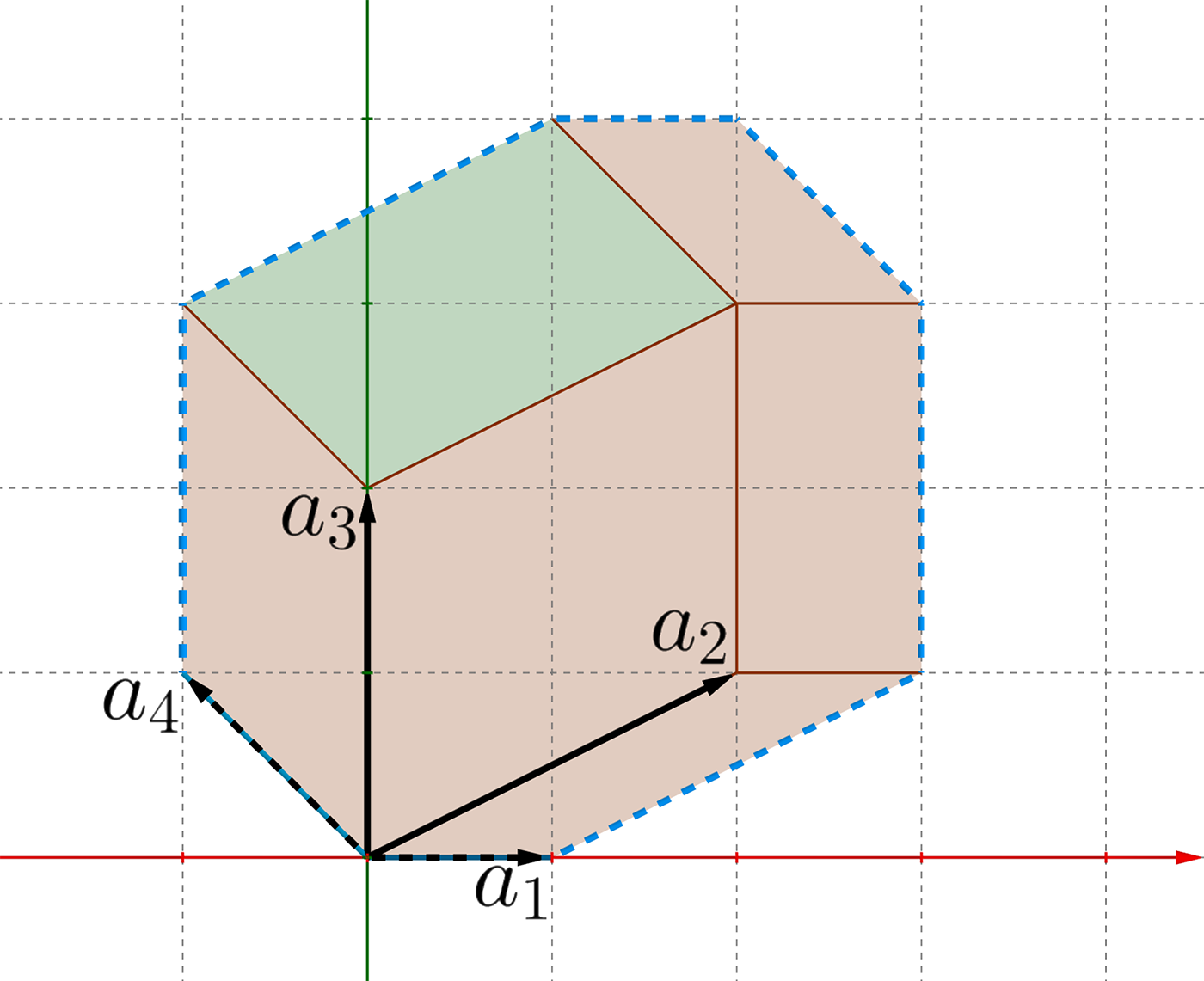
Les chercheurs de Zonotope hit-and-run for efficient sampling from projection DPPs se sont alors intéressés à un DPP particulier, un dé un peu bizarre qui correspond à un choix très particulier de vecteurs associés aux images, et que l’on peut tirer en un temps dérisoire grâce à un algorithme appelé « d’Aldous-Broder ». Les chercheurs ont recherché s’il existait d’autres DPP que ce cas exotique, c’est-à-dire d’autres façons de choisir les vecteurs associés aux images, pour lesquels cet algorithme pouvait fonctionner. En voulant généraliser cet algorithme rapide à des DPP plus généraux, les chercheurs ont eu besoin de la notion de zonotope. Dans cette nouvelle approche, au lieu de calculer directement les différentes surfaces, le zonotope serait le patron, la mise à plat de ce dé, que l’on pourrait explorer différemment. Les chercheurs ont ainsi pu exploiter une approche de type Monte-Carlo, qui explore les régions du patron les plus prometteuses en évitant de calculer les déterminants de toutes les faces du dé, ce qui réduit ainsi énormément les temps de calcul. 

La méthode proposée apporte la garantie mathématique de donner un résultat très proche d’un tirage de DPP, mais son coût calculatoire est encore incertain. Sur des exemples concrets, les chercheurs ont observé que leur méthode est plus rapide que l’état de l’art, mais il leur faut maintenant une preuve mathématique que leur méthode est plus rapide pour n’importe quel choix de vecteurs représentant des images, c’est-à-dire pour n’importe quelle mesure de pertinence et de diversité imposée par une application en apprentissage. Encouragés par leurs résultats, ils vont aussi essayer de généraliser encore la classe de DPP qu’ils peuvent tirer rapidement avec leur algorithme, pour tenter d’y inclure d’autres DPP utiles dans les applications d’apprentissage et de statistiques. En particulier, ils vont tenter de travailler avec des DPP correspondant à des dés avec un nombre infini de faces ! 

Publication
Zonotope hit-and-run for efficient sampling from projection DPPs de Guillaume Gautier1 , Rémi Bardenet2 , Michal Valko1

• 1 a b Équipe-projet commune Inria Sequel du Centre de Recherche en Informatique, Signal et Automatique de Lille (CRIStAL - CNRS/Université de Lille/École Centrale de Lille)
• 2 Centre de Recherche en Informatique, Signal et Automatique de Lille (CRIStAL - CNRS/Université de Lille/École Centrale de Lille)