La répulsion comme outil des détectives de la donnée, l’ERC Starting Grant de Rémi Bardenet
Les statistiques sont présentes dans un grand nombre de domaines scientifiques, avec bien souvent la nécessité de calculer des intégrales. Mais si conceptuellement c’est aussi simple que calculer un volume, le calcul pratique s’avère beaucoup plus compliqué, avec potentiellement des millions d’hypothèses à tester les unes après les autres… Pour répondre à ces problématiques dans des délais raisonnables, Rémi Bardenet souhaite intégrer un nouvel outil, les processus stochastiques répulsifs. Issus de la physique statistique et des probabilités, ces outils font depuis peu leur entrée en intelligence artificielle. Ces processus permettent de mieux mailler les zones dont il faut déterminer le volume, et ainsi de lancer moins de calculs.
Les simulations informatiques coûteuses sont devenues monnaie courante dans les sciences expérimentales. Les astrophysiciens conçoivent des modèles complexes de l'évolution des galaxies, les biologistes élaborent des modèles complexes de cellules, les écologistes modélisent la dynamique des écosystèmes à l'échelle mondiale. Au cœur de ces modèles, on trouve des équations qui décrivent le comportement observable des objets étudiés. Résoudre numériquement ces équations peut prendre des minutes, voire des heures avec le matériel actuel. Par ailleurs, toutes ces équations ont des paramètres physiques qu’on aimerait déterminer à l’aide de données observées. C’est le travail du statisticien, qui part des données afin de déterminer le modèle précis qui a pu les produire. Pour les statisticiens bayésiens, cela nécessite des millions de résolutions d’équations en série. « On se retrouve dans la peau de Sherlock Holmes, nous précise Rémi Bardenet, chargé de recherche CNRS au Centre de Recherche en Informatique, Signal et Automatique de Lille (CRIStAL - CNRS/Université de Lille/École Centrale de Lille). Nous avons nos indices, les données, et des hypothèses sur ce qu’il a pu se passer en réalité. C’est à moi d’aider les scientifiques à « remonter » des données à des mesures de crédibilité de chaque hypothèse, et ainsi déterminer les paramètres physiques et les modèles les plus en adéquation avec la réalité. » Cette démarche, appelée inférence statistique, conduit dans l’approche bayésienne à calculer une intégrale. « Si on simplifie, cela correspond à calculer avec précision le volume d’un objet tordu et découpé en morceaux irréguliers », indique le chercheur.
Concrètement, le chercheur est par exemple impliqué aux côtés de biologistes dans l’étude de cellules cardiaques pour la compréhension des réactions aux traitements de l’arythmie. En effet, les effets secondaires s’avèrent très difficiles à quantifier, le médicament au lieu de stabiliser le fonctionnement du cœur peut entraîner au contraire des emballements qui peuvent être fatals. « Les biologistes me fournissent les données expérimentales réalisées sur les cellules cardiaques, les 30 paramètres qui entrent en interaction dans l’électrophysiologie du cœur, ainsi qu’un ou plusieurs modèles de la façon dont les cellules cardiaques sont censées répondre aux stimulations électriques, liste Rémi Bardenet. À moi ensuite d’aider ces biologistes à définir les intégrales qui répondent à leurs questions, comme « Quel sont les meilleures équations pour décrire l’activité électrique de telle cellule ? » ou « Est-ce que tel médicament a pour effet secondaire de bloquer le passage de telle molécule importante ? ». À moi surtout d’aider les biologistes à lancer les calculs informatiques de ces intégrales, pour déterminer à partir des données observées ce qui s’est réellement passé dans la cellule. »
Pour trouver un ensemble de paramètres supportés par les données, il faut par exemple conceptualiser un espace à 30 dimensions, les 30 paramètres d’un modèle, où chaque point correspond à une réalité différente. Les données observées dans une cellule ne sont compatibles qu’avec une certaine zone de cet espace à 30 dimensions. Déterminer le volume de cette zone de paramètres permet de sélectionner le modèle qui explique le mieux ce qui s’est produit dans la cellule. Le problème c’est que pour avoir une bonne approximation de ce volume, il faut souvent calculer la compatibilité d’un million de réalités possibles de façon séquentielle, c’est-à-dire résoudre numériquement des équations qui gouvernent la cellule un million de fois à la suite. Avec une minute de calcul pour chaque résolution, cela donne à l’heure actuelle des calculs qui prendraient deux ans à se réaliser. « Ce n’est pas une échelle de temps acceptable pour pouvoir être utile aux biologistes ou aux astrophysiciens, s’emballe le chargé de recherche. Mon but est de ramener ce temps de calcul à quelques jours. »
Comment faire, alors ? En développant une méthode particulière de Monte Carlo : les « processus stochastiques répulsifs ». Le nom a de quoi faire fuir, ce qui amuse Rémi Bardenet : « C’est grâce à la répulsion que ces outils sont attractifs en intelligence artificielle ! » Dans de tels espaces de paramètres immenses, il faudrait pouvoir identifier rapidement la région des réalités les plus compatibles avec les données, et trouver approximativement son volume, en lançant le moins de calculs possibles. « C’est comme si l’espace à 30 dimensions était une grande boîte, dans laquelle nous lancions un million d’électrons, illustre le chercheur. Les électrons étant chargés négativement, ils se repoussent les uns les autres, ce qui permet qu’ils se répartissent partout dans la boîte et ne laissent aucun espace vide. Nous sommes ainsi certains de mailler efficacement l’espace. »
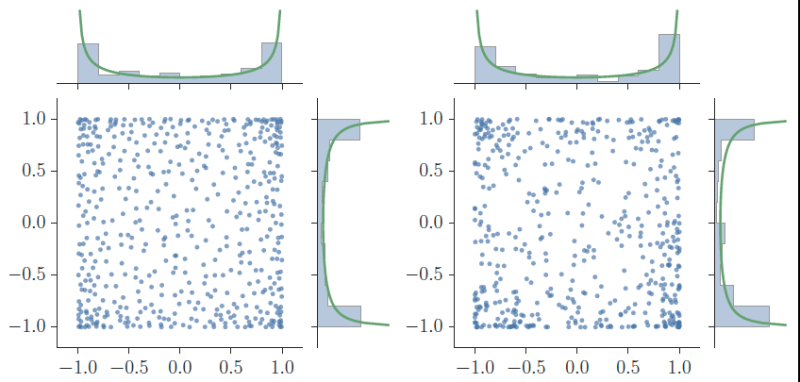
Grâce à ces processus répulsifs, et en particulier aux processus déterminantaux, on peut déterminer le volume pondéré d’une région de l’espace des paramètres d’un modèle en faisant la moyenne des compatibilités de tous les points - les « électrons » - qui se trouvent dans cette région. Mesurer la compatibilité de chaque point avec les données requiert toujours un long calcul, mais il est possible d’en réaliser moins pour la même marge d’erreur. « Je pense que c’est le bon moment pour se lancer dans cette thématique car les processus répulsifs ont été beaucoup étudiés par les mathématiciens depuis les années 2000, et il y a une vraie communauté qui se monte pour en faire des outils de calcul, se réjouit Rémi Bardenet. J’ai pu être là au tout début avec mon collègue mathématicien Adrien Hardy, avec qui nous avons assez tôt entrevu les possibilités computationnelles des processus répulsifs. Il s’agit maintenant de savoir s’ils peuvent être une révolution dans l’intégration numérique. »
