Le partage équitable, un casse-tête du gâteau au bureau

Félicitations. Un bâtiment flambant neuf vient d’être construit pour accueillir votre laboratoire à la rentrée prochaine. Vous devez désormais organiser la répartition des équipes dans les différents bureaux. Chaque équipe a ses propres préférences sur les bureaux, et la répartition finale doit en tenir compte. De même, chaque équipe doit obtenir un ensemble contigu de bureaux dans le bâtiment. C’est une contrainte forte : on imagine mal comment une équipe pourrait travailler dans de bonnes conditions si elle est éclatée sur plusieurs endroits dans le bâtiment. Vous avez affaire à un problème d’allocation équitable de ressources, sous contrainte de connexité. Bon courage. Mais les auteurs de la publication « Fair Division of a Graph » peuvent vous y aider. 

Le problème d’avoir à partager de manière équitable une ressource commune entre plusieurs individus, groupes, entités, est un problème auquel nous avons tous été confrontés un jour, et que l’on retrouve dans de nombreux contextes : partage de biens lors d’un héritage, allocation de travaux pratiques à des étudiants, attribution de droits d’exploitation sur une ressource naturelle, partage de terrains agricoles, co-exploitation d’une infrastructure scientifique commune… Les exemples ne manquent pas. 

Si ce type de problèmes intéresse naturellement les économistes depuis des décennies, les chercheurs en informatique s’y penchent sérieusement depuis quelques années. Pourquoi ? Tout d’abord, on retrouve naturellement certains de ces problèmes d’allocation de ressources dans le domaine informatique : allocation de bande passante dans des réseaux, partage de temps d’utilisation de processeurs… Les concepts de modélisation mathématique de l’équité proposés par les économistes fournissent des solutions intéressantes à ces problèmes. Ensuite, le domaine du partage équitable et plus généralement celui du choix social et de la prise de décision collective regorge de problèmes informatiques passionnants.

Dans le domaine du partage équitable, on distingue généralement deux types de cadres, selon la nature de la ressource à partager. Le premier de ces cadres est le partage d’une ressource continue. La métaphore employée généralement pour décrire ce type de problèmes est celle du « cake-cutting », qui peut s’exprimer comme suit : prenons un gâteau rectangulaire éventuellement hétérogène (1/3 chocolat, 1/2 fraise, 1/6 vanille) et un groupe de n amis ayant des goûts différents (x adore la vanille et déteste la fraise, y est indifférent entre tous les ingrédients…). Le groupe d’amis dispose d’un couteau ne pouvant faire que des coupes parallèles au petit côté du gâteau. Comment le groupe peut-il procéder pour couper le gâteau de manière à respecter certaines propriétés d’équité telles que la proportionnalité (chaque individu a l’impression d’avoir une part valant au moins le n-ème du gâteau entier) ou encore l’absence d’envie (aucun convive n’envie la part de quelqu’un d’autre, chacun préfère sa propre part) ? 

Le second paradigme classique dans le domaine des problèmes de partage est celui du partage équitable de biens indivisibles. Cette fois-ci, la ressource commune est un ensemble d’objets, dont chaque objet ne peut être coupé en plusieurs morceaux ni attribué à plusieurs individus à la fois. C’est dans ce cadre que se situe « Fair Division of a Graph ». Les problématiques de partage équitables ont déjà été bien étudiées, mais l’originalité de l’approche des chercheurs est la prise en compte d’une contrainte de connexité dans le partage. Formellement, les chercheurs considèrent que les objets à partager sont liés par une relation qui indique quel objet est voisin de quel autre, formant ainsi un graphe de voisinage (représentation informatique à base de points (des nœuds) et des traits (des arêtes) les reliant). Ils cherchent une allocation équitable des objets aux individus de telle manière que chaque individu reçoive un ensemble connexe d’objets. 

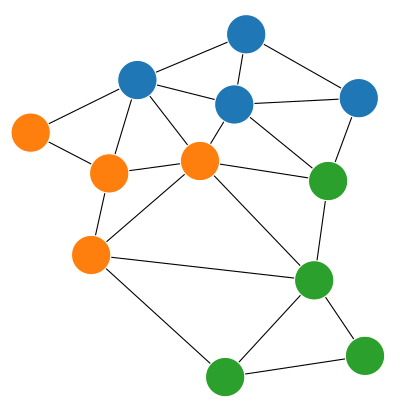
Ce graphe et cette contrainte de connexité permettent de modéliser de nombreux cadres naturels de partage. La relation de voisinage peut par exemple servir à modéliser la relation de contiguïté entre les bureaux évoquée dans l’exemple introductif. Ce graphe peut également servir à encoder la relation de voisinage spatial entre des parcelles de terrain que l’on doit attribuer à différents exploitants. Enfin, si le graphe est simplement un chemin linéaire, cette relation peut modéliser un axe temporel sur lequel les objets sont des créneaux d’utilisation d’une ressource par exemple. De manière intéressante, ce dernier cas peut également être vu comme l’analogue discret du paradigme du « cake-cutting » dans lequel nous ne pourrions couper notre gâteau qu’à un nombre fini d’endroits fixés à l’avance. Cette analogie a d’ailleurs été mise à profit pour découvrir certains résultats de l’article. 

Dans cet article, les chercheurs se sont intéressés à la complexité du problème consistant à déterminer s’il existe un partage équitable (pour plusieurs formalisations de l’équité, telles que la proportionnalité ou l’absence d’envie) satisfaisant la contrainte de connexité. Malheureusement pour votre problème de répartition d’équipes dans les bureaux, les chercheurs ont démontré que ce problème est difficile, même pour des graphes très simples (chemins linéaires par exemple). Est-ce à dire que la résolution de ce problème est sans espoir ? Pas forcément. Si votre graphe de voisinage est un arbre et si votre nombre d’individus concernés par le partage reste faible, il est possible de vous donner des méthodes de résolution efficaces (polynomiales), qui ne sont pas sans rappeler les protocoles de partage de gâteaux les plus prisés des économistes. Il ne vous reste plus qu’à borner le nombre d’équipes de votre laboratoire, et à déménager votre laboratoire dans un bâtiment organisé comme un arbre… 

Publication
« Fair Division of a Graph » de Sylvain Bouveret1 , Katarína Cechlárová2 , Edith Elkind3 , Ayumi Igarashi3 , Dominik Peters3

• 1Laboratoire d’Informatique de Grenoble (LIG, CNRS/Inria/Grenoble INP/Université Grenoble Alpes)
• 2P.J. Šafárik University, Slovakia
• 3 a b c University of Oxford, UK