Le calcul numérique est un outil essentiel dans l’automatisation d’un certain nombre de tâches : calcul d’images 3D dans les jeux vidéos, prévisions météorologiques, pilotage automatique de divers véhicules, commande d’appareils médicaux. Pour les tâches critiques impliquant la sécurité de personnes ou de biens, la survenue d’imprécisions ou le plantage de l’application est généralement inacceptable. Il faut donc des outils pour nous assurer de la fiabilité des systèmes développés et préciser avec certitude leur marge d’erreur.
On peut schématiquement regrouper les erreurs de calcul numérique en trois catégories. La première concerne les erreurs dues à l’arithmétique flottante. Puisqu’un ordinateur ne peut conserver qu’une quantité finie d’information, une solution consiste à approcher un nombre réel par un nombre flottant en ne gardant qu’un nombre fini de décimales. De même, les opérations arithmétiques (addition, soustraction, multiplication, division) sont dégradées en des opérations approchées sur les flottants, avec erreurs d’arrondi. La deuxième catégorie regroupe les erreurs de méthode que l’on rencontre dès qu’un problème trop compliqué (non linéaire, de dimension infinie…) doit être approché par une version simplifiée traitable en temps raisonnable par un ordinateur, amenant ainsi une seconde source d’erreurs. Enfin, la troisième catégorie contient toutes les erreurs dues à une mauvaise implémentation des algorithmes ou à une défaillance physique du matériel utilisé pour le calcul.
Bien que certaines de ces erreurs puissent sembler anodines, une trop grande sensibilité du problème aux perturbations ou la nécessité d’itérer le calcul un grand nombre de fois peuvent vite faire apparaître des comportements aberrants. Identifier la source de ces erreurs est un processus long et délicat, le plus souvent réalisé à l’aide d’une coûteuse phase de test.
Le calcul numérique certifié (rigourous numerics en anglais) désigne tout un ensemble de méthodes permettant de contrôler ces erreurs. C’est le cœur de métier d’une partie de l’équipe AriC du LIP [1]. Une des briques de base les plus couramment employées est l’arithmétique d’intervalles, dans laquelle on remplace une valeur réelle par un intervalle (avec des flottants pour extrémités). Les opérations élémentaires peuvent alors s’étendre aux intervalles avec la garantie que l’intervalle de sortie contienne toujours le résultat recherché. Cela permet déjà de contrôler les erreurs d’arrondis (première catégorie) en encadrant de manière rigoureuse la vraie solution mathématique. On parle de méthodes auto-validantes, puisque ce calcul garantit en soi la pertinence du résultat.
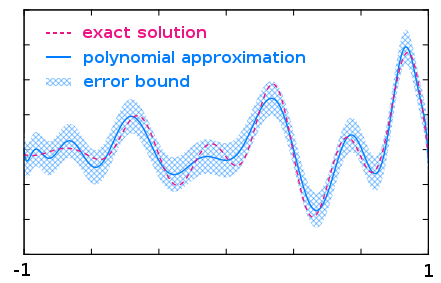
D’autres outils permettent de contrôler les erreurs de la deuxième catégorie. Par exemple, pour approcher sur machine des fonctions mathématiques, on recourt fréquemment à des approximations polynomiales, des objets à la fois simples et universels qui s’évaluent à l’aide des opérations arithmétiques + et x. Leur contrepartie rigoureuse consiste en des approximations polynomiales assorties d’une borne d’erreur permettant d’être certain d’encadrer la fonction mathématique de départ. Si les opérations élémentaires comme l’addition ou la multiplication se transposent facilement, la situation est différente pour des opérations plus compliquées, ne serait-ce que pour la division. Une bonne approche consiste alors à traiter le problème en deux temps : on commence par trouver une approximation de la solution grâce à des méthodes classiques de l’analyse numérique, puis on recalcule la borne d’erreur après coup (on parle de méthodes « a posteriori »), souvent grâce à des arguments topologiques reposant sur des théorèmes de point fixe.
Les erreurs de la troisième catégorie sont contrôlées grâce à des méthodes formelles, typiquement utilisées et développées au sein de l’équipe Plume du LIP. Contrairement aux techniques de test, qui ne font qu’attester la présence de bugs, les méthodes formelles permettent de garantir leur absence. Dans ce domaine, l’assistant de preuve Coq est un outil très utilisé, permettant de formaliser des preuves mathématiques et de les vérifier automatiquement. Cet outil est particulièrement intéressant pour les preuves de programmes, qui sont bien souvent trop fastidieuses pour être vérifiées manuellement.
Florent Bréhard est actuellement doctorant et travaille à l’interface de ces deux équipes et de l’équipe MAC du Laboratoire d’Analyse et d’Architecture des Systèmes (LAAS-CNRS). Il est coencadré par Nicolas Brisebarre (LIP, équipe AriC), Damien Pous (LIP, équipe Plume), et Mioara Joldes (LAAS-CNRS, et ancienne doctorante du LIP). Ensemble, ils ont récemment conçu un algorithme de validation pour des solutions approchées en base de Tchebychev d’équations différentielles ordinaires linéaires [2]. Cette méthode a été appliquée avec succès à la validation de trajectoires de satellites lors du problème dit de rendez-vous spatial [3], ainsi qu’au calcul rigoureux d’intégrales abéliennes. Ces dernières ont permis, dans le cadre du seizième problème de Hilbert, de construire un champ de vecteur polynomial de degré 4 possédant 24 cycles limites [4]. La formalisation en Coq de ce dernier résultat est en cours.
Publications :
- FastRelax : fast and reliable approximation, project funded by the ANR, 2014-2018.
- Florent Bréhard, Nicolas Brisebarre, Mioara Joldes. Validated and Numerically Efficient Chebyshev Spectral Methods for Linear Ordinary Differential Equations. ACM Transactions on Mathematical Software (TOMS), 2018, vol. 44, no 4, p. 44.
- Paulo Ricardo Arantes Gilz, Florent Bréhard, Clément Gazzino. Validated Semi-Analytical Transition Matrix for Linearized Relative Spacecraft Dynamics via Chebyshev Polynomials. In : SCITECH 2018-AIAA Science and Technology Forum and Exposition, 28th Space Flight Mechanics Meeting. American Institute of Aeronautics and Astronautics, 2018. p. 1-23.
- Florent Bréhard, Nicolas Brisebarre, Mioara Joldes, Warwick Tucker. A New Lower Bound on the Hilbert Number for Quartic Systems. Preliminary version.
